무브

오르비

아톰

내 태그

내 태그 설정

입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion

입시크릿 [988675] · MS 2020 · 쪽지

2020-10-09 21:39:51
조회수 3,505

【바보의 수학-문제풀이】 2019 수능 수학 가형 30번 분석

게시글 주소: https://m.orbi.kr/00032578175

안녕하세요, 입시크릿입니다.


이번 칼럼에서는 2019년에 실시된 2020학년도 수능 수학 가형 (이과) 30번 문제에 대한 ebs풀이와 함께 저의 조금 다른 풀이방법을 제시해보겠습니다.


단순한 해설지는 여러 다른 사이트에서도 충분히 확인할 수 있으므로, 단순한 풀이방법을 넘어 왜 이렇게 문제를 푸는지, 논리적 사고를 하는 방법을 알려드리겠습니다.


저의 이전 '바보의 수학' 칼럼에서 알려드린 수학 공부법을 토대로 하므로 안 읽어보신 분은 한 번 읽고 오시는 것도 도움이 될 것입니다.


(더많은 칼럼과 공부법을 https://blog.naver.com/epsecret 에서 만나보세요)





먼저 30번 문제와 함께 해설지에서 제시한 풀이방법을 살펴보겠습니다.




해당 풀이는 ebsi에 업로드 되어있는 30번 해설지의 일부입니다.


답지를 보지 않고 문제를 푸는 학생도, 답지를 봐도 이해를 하기가 어려운 학생도 있겠지만,


대부분 학생의 경우 "풀이가 이해는 된다. 근데 어떻게 저렇게 똑똑한 생각을 할 수 있는지 모르겠다. 비슷한 문제가 나오면 못풀것 같다." 라는 생각을 합니다.


따라서 과정 하나하나를 분석하며 풀이방법을 생각해내는 근거가 무엇인지, 어떤 방식으로 문제를 풀고 답지를 분석해야 실력이 늘 수 있을지 알려드리겠습니다.




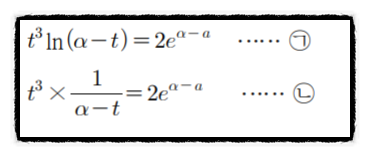
우리가 첫번째로 생각해 내야하는 것은 ㄱ,ㄴ식입니다.


"두 함수가 오직 한점에서 만난다." 라는 것은 미적분에서 매우 많이 쓰이는 성질이죠.


두 함수가 오직 한점에서 만나는 경우에는,


1. 함수값이 같다.

2. 해당 점에서의 미분계수가 같다.


를 통하여 ㄱ,ㄴ을 충분히 유도해 낼 수 있습니다.


이 두가지를 생각해내기가 힘들다면 문제를 풀며 응용력을 기르는 것보다는 그전에 개념공부를 하는 것에 더 비중을 두시는 것이 좋습니다.





이 30번문제의 진짜 어려움은 이 다음에 있다고 생각합니다. 아래 풀이를 읽어보기 전에 먼저 스스로 문제를 풀어보는 것을 추천드립니다.



풀이를 읽으면 이 방법이 모순이 없는 올바른 풀이라는 것은 이해할 수 있지만, 최상위권을 제외하면 답지를 보면서 의문점이 생기는 것이 당연합니다.


1. 저는ㄱ,ㄴ을 구한 다음에 무엇을 해야할지 모르겠던데, 갑자기 ㄱ의 식을 t에 대해서 미분한 이유가 뭔가요?

2. 저라면 ㄱ,ㄴ을 구한 후 두 식을 연립할 것 같습니다. 갑자기 ㄴ도 아니고 ㄱ을 왜 미분할까요?

3. 가만히 있는 3t2을 더 간단한 식도 아니고, 오히려 복잡하게 t3*(3/t) 으로 바꾸는 이유가 뭔가요?







맞습니다. 탁월한 일부 학생을 제외하면 ㄱ을 미분해야겠다는 생각이 잘 들지 않습니다.


저 역시도 마찬가지였으며, 항상 식을 유도한 이후에는 내가 유도해낸 수식이 어떤 성질이 있는지 살펴봐야 합니다.


ㄱ,ㄴ 두식을 보면 우변이 정확히 일치하고, 좌변에 공통적으로 t3이 있습니다.


즉 다음 과정은 2번 질문에서 말씀하신 그대로 공통인수를 최대한 지울 수 있도록 ㄱ,ㄴ을 연립하는게 맞습니다.



마찬가지로 이번에도 식을 변형했으므로 내가 유도해낸 식이 어떤 의미를 가지고 있는지, 특별한 성질이 있는지 다시 한번 살펴봐야 하겠죠?


ln x를 미분하면 1/x 입니다. 즉, 좌변을 미분하면 우변(-t이므로 부호는 바뀝니다)이 됩니다.


이 성질을 이용하면 첫번째 의문점, 왜 ㄱ을 미분하는지 알 수 있습니다. 


ln을 미분해도 위 성질에 의하여 다시 문자를 통일시킬 수 있기 때문에, ㄱ식을 미분하면 문자가 통일되어 식이 매우 간단해지는 것이 확실해졌기 때문입니다.


문제에서 준 식만을 바탕으로 바로 ㄱ을 미분하는 것은 쉽지 않습니다.


식을 다양하게 변형해보며 올바른 다음과정이 무엇일지 스스로 생각해 보아야 합니다.


해설지에서는 올바른 풀이를 제시하지만 그것을 생각해내는 방법을 가르쳐주지 않습니다. 그렇기 때문에 단순히 단순히 답지만 봐서는 실력이 늘지 않는 것입니다.









마지막으로 세번째 질문에 대한 답변을 드리면, 저는 출제자가 이미 답을 알고 있기 때문에 이러한 풀이방법을 선택했다고 생각합니다. 


저희는 답을 미리 아는 상황이 아니기 때문에, 똑똑한 사람들을 제외하면 바로 풀이처럼 생각하기는 어렵습니다.


위의 제 풀이가 기존 해설지보다 1~2줄 더 복잡할 수 있겠지만, 굳이 답지처럼 변형시키지 않아도 ㄱ을 미분해서 식을 쭉 정리하기만 해도 문제를 해결할 수 있습니다.


반드시 3t2을 t3 x 3/t으로 변형할 필요는 없다는 것이죠.






이렇게 킬러문제로 유명한 수능 수학 30번 문제라 해도 하나씩 하나씩 따지다 보면 크게 어렵지 않게 문제를 풀어낼 수 있습니다.


저의 풀이 방법과 문제 풀이 이론이 여러분께 도움이 되었길 바라며 이만 마치도록 하겠습니다.


감사합니다. :)

0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

입시크릿 [988675]

쪽지 보내기


  • 첫번째 댓글의 주인공이 되어보세요.
글쓰기
오르비 1366376번째 회원 가입
ddna
1,422,072 건의 게시물이
블록체인에 디지털 공증되었습니다.
901,751
497,321
22,267
574
159

오늘의 추천 글

2026 수능D - 321

오르비 플레이

오르비 RARE

오르비 과외시장
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2024 Move Inc.

orbisoptimus (v17-7e2515)