2020년 10월 모의고사 수학 가형 30번 해설
게시글 주소: https://m.orbi.kr/00033283858
오늘은 한달 전 시행됐던 10월 모의고사 수학 가형 (이과) 30번 문제 풀이방법에 대하여 알려드리겠습니다.
단순히 한 문제에 대한 풀이로 마치는 것이 아니라 문제를 푸는 근본적인 방법에 대하여 조언해드리니, 킬러문제가 고민이신 분들은 꼭 칼럼을 꼼꼼히 읽어주세요.
먼저 2020년 10월 모의고사 수학 가형 30번 문제를 소개합니다. 아직 문제를 풀어보지 않은 분들은 반드시 풀이를 보기전에 스스로 문제를 풀어보세요.
다음으로, ebsi에 수록되어 있는 공식 풀이방법을 소개해드리겠습니다.
물론 쉬운 문제는 아니였습니다. 그러나 킬러문제중 가장 어렵기로 유명한 30번의 평균 난이도를 고려하면 다른 30번들 보다는 쉬운 편이라 할 수 있습니다.
따라서 30번에 도전하려는 마음가짐으로 이 칼럼에 들어오신 여러분들이라면, 스스로 풀지는 못했더라도 답지 풀이 정도는 충분히 이해하실 수 있을 것입니다.
그러나 항상 가장 중요한 것은 단순 이해를 넘어서, 비슷한 문제가 나오면 내가 스스로 풀 수 있을지, 풀이를 온전히 내 것으로 만들 수 있을지 생각해 보는 것입니다.
지금부터 풀이과정을 하나씩 구체적으로 살펴보며 풀이를 여러분의 것으로 만들 수 있도록 도와드리겠습니다.
첫번째로, f(0) = f(-2)임을 문제에서 제시했습니다. 이차함수이기 때문에 숙련된 분들은 성질을 이용하여 f(x) = kx(x+2) + q 라고 바로 잡을 수 있을 것입니다.
그러나 제가 바람직하다고 평가하는 합리적인 풀이는, 공식 답지처럼 조금 돌아가더라도 "누구나 생각해낼 수 있는 아이디어"입니다.
따라서 바로 식을 잡기가 어렵더라도, f(x)에 0,-2를 대입하여 식을 전개해도 전혀 문제가 없으며 동일한 결론을 유도해 낼 수 있습니다.
첫번째 과정을 통하여 p를 k에 대하여 나타내는 데 성공했습니다. AB < 0 의 형태가 나왔네요. 따라서 두번째로 -1을 기준으로 x 의 범위를 나누는 것은 당연합니다.
아마 대부분의 분들이 아직까지는 의문이 들지 않을 것입니다. 문제는 다음 파트에서 발생합니다.
풀이 자체를 이해하는 분들은 제법 계실 것입니다. 그러나, g'(-1)=-2을 구하는데 갑자기 g', g"을 구하는 이유는 무엇인가요?
그리고 비슷한 문제가 나왔을때 우리는 똑같이 논리를 전개하여 문제를 풀어낼 수 있을까요? 지금부터는 합리적인 논리 전개 방법에 대하여 말씀드리겠습니다.
첫번째로, 우리는 우리가 유도한 이 식을 어떻게 사용할지 고민해봐야 합니다. g(x)가 x = -1의 전후로 mx+m이라는 식과 부호가 바뀌려면 어떻게 해야할까요?
우선 x에 -1을 대입해 g(-1) = -m+m 값이 나와야 합니다. 그래야 부호가 바뀔 수 있는 최소한의 조건이 만족됩니다. 즉 첫번째 식 g(-1) = 0 이 유도됩니다.
그러나 여기서 우리는 하나의 식을 더 생각해내야 합니다. 왜냐하면 g(-1) = 0 은 필요조건일 뿐이지, g(-1) = 0 이라고 해서 주어진 부등호가 반드시 성립하는 것이 아니기 때문입니다.
여기에 식을 만족시키려는 m의 최소값이 2라는 힌트가 주어져 있습니다. 즉 이 식을 이용하여 추가 조건을 구하라는 것을 깨달을 수 있습니다.
저는 이후의 풀이는 공식 풀이와는 조금 다른 방식으로 해결했습니다. 생각해보세요. -1을 기점으로 mx+m와의 대소가 변하려면 어떻게 해야할까요?
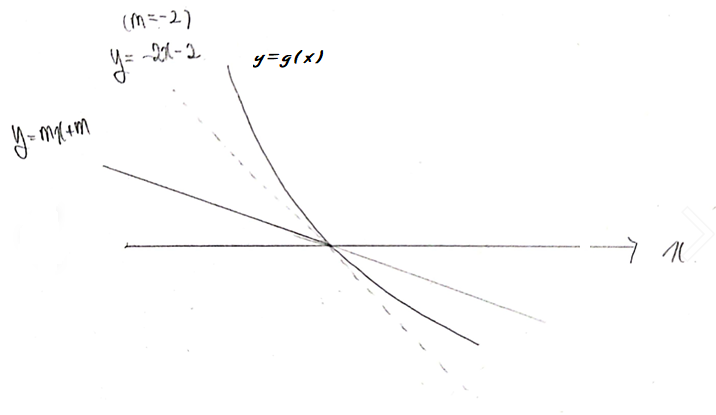
반드시 그림과 같은 형태가 나와야합니다. 즉 함수값이 같은 것 뿐만 아니라 반드시 m이 g'(-1)보다는 크거나 같아야 한다는 것이죠. 이때 m의 최소값이 -2이므로, g'(-1) = -2 가 되는 것은 자명합니다.
이제 두 식을 연립하여 다음 식을 유도할 수 있습니다.

이 식은 문자 3개, 식1개의 형태입니다. 즉 2개의 식만 더 있으면 문제를 풀어낼 수 있습니다. 이제 (나)식을 한번 살펴볼까요?
(나) 조건은 딱 두개의 식을 구할 수 있도록 되어 있습니다. 또한 g(x)는 지수 위의 식을 미분하면 아래의 함수가 나오는 형태기 때문에, 매우 적분하기 쉽습니다.
따라서 이제 문자 3개, 식3개, a,k,q를 모두 구할 수 있다는 것입니다. 문제의 풀이를 단순히 쭉 읽어봤을때는 스스로 풀기가 어렵다고 생각할 수 있습니다.
그러나 하나씩 과정을 살펴보며 왜 이런 아이디어를 사용 할까?에 초점을 맞추어 복습을 한다면, 문제를 푸는 것이 점점 쉬워진다는 것을 느낄 수 있습니다.
여러분들 스스로도 "내가 왜 이러한 방식으로 논리를 전개해나가고 있을까" 라는 질문을 스스로 던지며 문제를 풀어보세요. 근본적인 실력이 크게 향상될 것입니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
근데 나는 0
수능을 봐서 혼자인거임 그렇게 믿고싶음
-
강기본 해야함? 0
지금 강민철로 독서 급하게넘어왔는데 강기본해야함?? 현역이고 이번수능 국어 3등급 후반임
-
너무 빨라요…. 3
준비 완료… 졸사 증사 졸업식 인터뷰 영상 순입니다
-
어떤 느낌으로 풀지 궁금하네
-
무물 1
이라해도 질문 잘 안쓰더라... 그래도 심심하니까 해볼게
-
그만할게
-
ㄹㅇ ㅋㅋ
-
당신이 연애를 못한다면 그건 그냥 안하고 있거나 노력을 안하고 있는 겁니다.
-
ㅋㅋㅋ
-
어려움
-
외모 무 재산 무 학벌 무 여친 무 Joat인생
-
일단 나부터
-
확통런 고민 3
언미+사탐 작수 미적 84(미적 3틀) 총 등급 12231 내신으로 확통해봄 의견 오네가이시마스
-
맞팔구 3
동테 위기입니다
-
연애시절 카톡 ㅇㅈ 20
미방용 모아이 기만좀 하고싶었음 아무튼 못생겨도연애는한다~
-
캬캬 0
내일부터 피와 눈물의 공부머신이 될거야 캬컄 월~수 공부 시간 조졌네 조졌어
-
보통 거의 학벌은 갖춰져있음 근데 갑자기 외모까지 갖춘 사람들이 ㅈㄴ 나타남 왜...
-
ㄹㅇ
-
ㅇㅂㄱ 12
-
약대나 의대나 11
다 같이 웃고 떠들던 연뱃이었는데 나만....어째서 나만.....
-
1시 전까지 돌파하지 않는다면 없던 걸로 하겠습니다 [좋아요 50개 넘으면 이따...
-
제발 빨리 떠라 학고우편 오기전에 자퇴해야해~~
-
반수 망했다면 어땠을까 라는 바보같은 생각이 들기도함 님들은 이런생각 안해봄?
-
ㅇㅈ하고 수린이한테ㅜ밖에 쪽지를 못 받아봄…
-
메가에서 ebs연계대비강좌 ㅊㅊ좀요
-
근데 요즘 3시에 잠 。◕‿◕。 。◕‿◕。 。◕‿◕。 。◕‿◕。 。◕‿◕。...
-
대학도 씹고트인데 얼굴도 씹고트면 너무나도 부러워짐 난 좀 보내줘라
-
정말 순수하게 착한 사람이 있어 가식적인 게 아니라 선의로 가득한 언제나 배려심...
-
으흐흐흐흐 오늘 새벽에 보고있다가 나중에 캠퍼스에서 옯비언들 특정해야지
-
어젠 다행히도 내 키는 넘음
-
내 돈 내놔…
-
남친 자리는 비었나요?
-
오늘 아이패드를 샀기때문 으흐흐흣
-
직장상사에서 애인으로
-
하는 유형이 나오면 보통 수능에서 킬러인가요?
-
동국대 법학 vs 경희대 국문
-
.
-
내가 잘생겼다면 4
세상이 조금은 더 밝아보였을까
-
이제 왔는데 2
ㅇㅈ메타 다 끝났네…에휴다뇨…
-
찐친->사랑
-
보지 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ
-
개강하고날잡는다
-
못생겨서 죄송합니다 17
사죄드려요
-
날개야 다시 돋아라. 날자. 날자. 날자. 한 번만 더 날자꾸나. 한 번만 더 날아 보자꾸나
-
농어촌 질문 1
발뻗잠 가능할까요? 과컷은 안 걸리고 85명 지원 // 40명 선발 // 47명 점공 참여네요…
-
부러우니까
-
분명 낮에 일할때랑 일하는시간은 같은데 자는시간은 더..늘어남..
-
저 1학년1학기에 학급회장했는데..이걸로 제가 학급 회장이었던거 입학사정관들이...






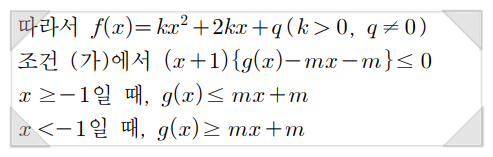

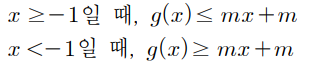



















































이따가 공부 끝내고 읽어볼게요